A. Tabung
1. Melukis Jaring-jaring Tabung
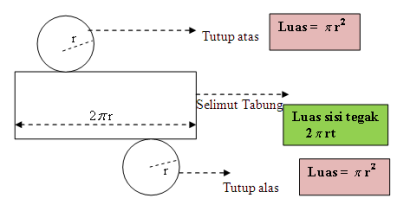
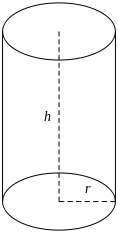
a. Jaring-jaring Tabung
Tabung atau silinder tersusun dari tiga buah bangun datar, yaitu:
a. Selimut tabung yang berupa persegi panjang, dengan panjang selimut sama dengan keliling lingkaran alas tabung 2πr dan lebar selimut sama dengan tinggi tabung t.
b. Dua lingkaran dengan jari-jari r.
Gambar diatas menunjukkan jaring-jaring sebuah tabung dengan jari-jari alas dan atapnya yang berupa lingkaran adalah r dan tinggi tabung adalah t.
2. Menghitung Luas Selimut dan Volume Tabung
a. Luas SelimutLuas seluruh permukaan tabung atau luas sisi tabung merupakan jumlah dari luas alas ditambah luas selimut dan luas atap.
Sehingga dapatkan rumus:


b. Volume Tabung
volume tabung adalah perkalian luas daerah lingkaran alas dengan tinggi tabung.

B. Kerucut
1. Melukis Jaring-jaring Kerucut
Kerucut tersusun dari dua bangun datar, yaitu lingkaran sebagai alas dan selimut yang berupa bidang lengkung (juring lingkaran). Kedua bangun datar yang menyusun kerucut tersebut disebut jaring-jaring kerucut.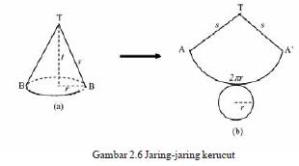
Gambar diatas menunjukkan kerucut dengan jari-jari lingkaran alas r, tinggi kerucut t, apotema atau garis pelukis s.Jaring jarring kerucut terdiri dari:
a. selimut kerucut yang berupa juring lingkaran dengan jari-jari s dan panjang busur 2πr,
b. alas yang berupa lingkaran dengan jari-jari r.
2. Menghitung Luas Selimut dan Volume Kerucut
a. Luas SelimutLuas seluruh permukaan kerucut atau luas sisi kerucut merupakan jumlah dari luas juring ditambah luas alas yang berbentuk lingkaran.
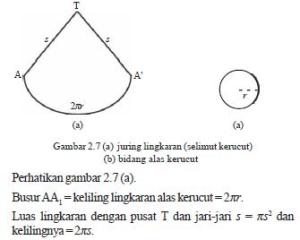
Lp = luas selimut + luas alas kerucut
= πrs + πr2
= πr (s + r)
Jadi
dengan r = jari-jari lingkaran alas kerucut
s = garis pelukis (apotema)
b. Volume Kerucut
Hubungan antara r, t dan apotema (s) adalah s2 = r2 + t2
C. Bola
1. Menghitung Luas Selimut dan Volume Bola
Luas selimut atau permukaan (sisi) bola. Jika jari-jari alas tabung tersebut r dan tingginya sama dengan diameter d, maka luas selimut atau sisi bola dengan jari-jari r adalah: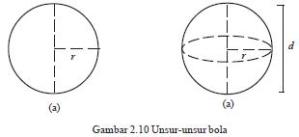
2. Menghitung Luas Selimut dan Volume Bola
Sebelum mempelajari luas selimut dan volume bola, lakukanlah kegiatan berikut.
Ternyata dari kegiatan di atas kita dapat merumuskan luas selimut
atau permukaan (sisi) bola. Jika jari-jari alas tabung tersebut r dan
tingginya sama dengan diameter d, maka luas selimut atau sisi bola
dengan jari-jari r adalah:
D. Hubungan Volume Bangun Ruang Sisi Lengkung dengan Jari-jari
1. Perbandingan Volume Tabung, Kerucut, dan Bola karena Perubahan Jari-jari
a. Perbandingan Volume TabungDua buah tabung dengan tinggi yang sama, tetapi jari-jari berbeda, maka perbandingan kedua volume tabung sama dengan perbandingan kuadrat masing-masing jari-jarinya.
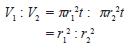

b. Perbandingan Volume pada Kerucut
Dua buah kerucut dengan tinggi sama, tetapi jari-jari alasnya berbeda, maka perbandingan volume kedua kerucut dengan perbandingan kuadrat masing-masing jari-jarinya.

c. Perbandingan Volume pada Bola
Dua buah bola dengan jari-jari yang berbeda, maka perbandingan volumenya sama dengan perbandingan di pangkat tiga dan masing-masing jari-jarinya



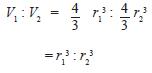

Tidak ada komentar:
Posting Komentar