Sebelum kita mempelajari bagaimana
metode dalam menyelesaikan siste persamaan linier , maka kita harus
memahami terlebih dahulu mengenai definisi kalimat terbuka dan definisi
persamaan serta tentang sistem persamaan linier . Sehingga dalam
menyelesaikan persamaan linier kita tidak bingung.
Kalimat Terbuka , yaitu suatu kalimat yang memiliki atau memuat variabel .
Sumber : http://rumusrumus.com/sistem-persamaan-linier/
A. Pengertian Kalimat terbuka , persamaan dan persamaan linier
Kalimat Terbuka , yaitu suatu kalimat yang memiliki atau memuat variabel .
Persamaan , yaitu kalimat terbuka yang menyatakan hubugan sama dengan ( = ) .
Persamaan Linier ,
yaitu suatu persamaan yang setiap sukunya mengandung konstanta dengan
variabelnya berderajat satu ( tunggal ) dan persamaan ini , dapat
digambarkan dalam sebuah grafik dalam sistem koordinat kartesius .
Suatu Persamaan akan tetap bernilai
benar atau EKWIVALENT ( < = > ) , Apabila ruas kiri dan ruas kanan
ditambah atau dikurangi dengan bilangan yang sama .
Bentuk umum persamaan linier :
y = mx + b
Contoh bentuk persamaan linier :
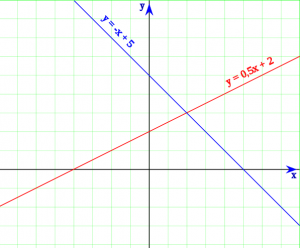
y = -x + 5
y = -05x + 2
Contoh bentuk grafik persamaan linier :
Dari gambar di atas , dapat kita
simpulkan bahwasannya m atau gradiennya = 0,5 dan b atau titik potong
sumbu y = 2 ( pada garis merah )
B. Metode Penyelesaian Persamaan Linier
Ada beberapa metode yang dapat digunakan
dalam menyelesaikan sebuah permasalahan persamaan linier , metode –
metode tersebut adalah :
a. Metode Substitusi
b. Metode Eliminasi
c. Metode Campuran ( eliminasi dan substitusi )
d. Metode grafik
Berikut adalah penjelasan lebih rinci mengenai metode penyelesaian persamaan linier :
- Metode Substitusi
Metode subsitusi yaitu metode atau cara
menyelesaikan persamaan linier dengan mengganti salah satu peubah dari
suatu persamaan dengan peubah yang diperoleh dari persamaan linier yang
lainnya .
Untuk lebih jelasnya lagi , perhatikan contoh berikut ini :
Diketahui persamaan x + 3y = 7 dan 2x + 2y = 6 , tentukan Himpunana Penyelesaiannya :
Penyelesaiannya :
x + 3y = 7
< = > x = -3y + 7 . . . .( 1 )
Lalu , masukkan persamaan ( 1 ) ke dalam persamaan ( 2 ) untuk mencari nilai y
2x + 2y = 6
< = > 2 ( -3y + 7 ) + 2y = 6
< = > -6y + 14 + 2y = 6
< = > -6y + 2y = 6 – 14
< = > -4y = – 8
< = > y = 2
Gunakan persamaan antara persamaan ( 1 ) atau ( 2 ) untuk mencari nilai x
x + 3y = 7
< = > x + 3 ( 2 ) = 7
< = > x + 6 = 7
< = > x = 1
Jadi , HP = { 1 , 2 }
2. Meode Eliminasi
Metode Eliminasi , yaitu metode
penyelesaian sistem persamaan linir dengan cara mengeliminasi atau
menghilangkan salah satu peubah dengan menambahkan atau mengurangkan
dengan menyamakan koefisien yang akan dihilangkan tanpa memperhatikan
nilai positif atau negatif .
Apabila peubah yang akan dihilangkan
bertanda sama , maka untuk mengeliminasi menggunakan sistem operasi
pengurangan . Dan sebaliknya apabila peubah yang akan dihilangkan
bertanda berbeda , maka untuk mengaliminasi menggunakan operasi
penjumlahan .
Utuk lebih jelasnya , perhatikan contoh berikut ini :
Masih dengan contoh yang sama , namun dengan cara yang berbeda yaitu :
Diketahui dua persamaan x + 3y = 7 dan 2x + 2y = 6 , tentukan HP dari persamaan tersebut !
Langkah pertama adalah lakukan eliminasi
dengan mengurangkan untuk menghilangkan peubah atau koefisien x untuk
mengetahui nilai y
2x + 2y = 6 : 2
< = > x + y = 3
lalu , lakukan
x + 3y = 7
x + y = 3 _
2y = 4
y = 2
Langkah selanjutnya adalah lakukan
eliminasi dengan mengurangkan untuk menghilangkan peubah atau koefisien y
untuk mengetahui nilai x
2x + 2y = 6 | x3 | < = > 6x + 6y = 18
x + 3y = 7 | x 2 | < = > 2x + 6 y = 14 _
4x + 0 = 4
x = 1
Jadi , Himpunan penyelesaian yang dihasilkan sama yaitu HP = { 1 , 2 }
3. Metode Campuran ( antara eliminasi dan substitusi )
Yang dimaksud dari metode ini , yaitu
kita dalam mencari himpunan penyelesaian menggunakan dua metode boleh
gunakan eliminasi terlebih dahulu setelah diketahui salah satu nilai
peubah baik itu x atau y maka selanjutnya masukkan ke dalam metode
substitusi atau sebaliknya .
Untuk lebih jelasnya , perhatikan contoh berikut :
Diketahui dua persamaan x + 3y = 7 dan 2x + 2y = 6 , tentukan HP dari persamaan tersebut !
Langkah pertama lakukan metode eliminasi , untuk mecari nilai x
2x + 2y = 6 | x3 | < = > 6x + 6y = 18
x + 3y = 7 | x 2 | < = > 2x + 6 y = 14 _
4x + 0 = 4
x = 1
Selanjutnya substitusikan nilai x ke dalam salah satu persamaan :
x + 3y = 7
< = > 1 + 3y = 7
< = > 3y = 7 – 1
< = > 3y = 6
< = > y = 2
Maka hasilnyapun sama yaitu HP = { 1 , 2 }
4. Metode Grafik
Metode grafik , yaitu dengan
menggambarkan dua persamaan pada grafik kartesius , dan himpunan
penyelesaiannya dihasilkan dari titik potong dari kedua garis tersebut .
Yang perlu diperhatikan yaitu ketika menggambar titik sumbu
kartesiusnya harus sama dan konsisten .
Untuk lebih jelasnya perhatikan gambar grafik berikut :
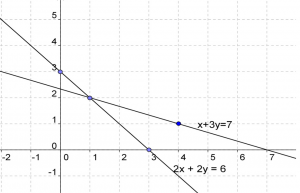
Gambarlah grafik persamaan x + 3y = 7 dan 2x + 2y = 6 , dan tentukan titik potongnya
Dari gambar di atas , maka kita dapat
melihat bahwa titik potongnya berada pada titik { 1 , 2 } dan dengan
kata lain HP = { 1 , 2 }
Demikian penjelasan mengenai sistem persamaan linier dan metode penyelesaiannya
. Semoga dengan penjelasan diatas kita dapat lebih faham mengenai apa
itu sistem persamaan dan cara – cara dalam menyelesaikannya . Untuk
memudahkan dalam menyelesaikan sistem persamaan , langkah yang pertama
yaitu memahami bentuk dari persamaan linier itu sendiri dan selanjutnya
kita fahami cara – caranya . Semoga bermanfaat dan dapat membantu
permasalahan dalam menyelesaikan persamaan linier .